What is MHD Power Generation
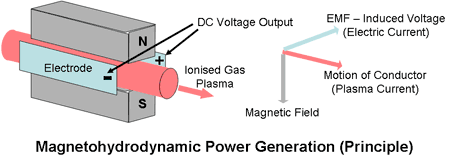
What is MHD Power Generation
Advantage of MHD Power Generation
(1) The conversion efficiency of an MHD system can be around 50 percent as compared to less than 40 percent for the most efficient steam plants.
(2) Although the costs cannot be predicted very accurately, yet it has been reported that capital costs of MHD plants will be competitive with those of conventional steam plants.
(3) Because of higher efficiency, the overall generation cost of an MHD plant will be less. It has been estimated that the overall generation cost in an MHD plant would be about 20% less than in convection steam plants.
(4) The higher efficiency means better fuel utilization. The reduced fuel consumption would offer additional economic and social benefits and would also lead to conversion of energy resources.
(5) The efficient heat utilization would decrease the amount of heat discharged to environment and the cooling water requirement would also be lower.
(6) The research studies at Aveo Everett Research Laboratories (USA) and other institutions have show that the use of precipitator not only recover the seed material but also effectively traps most other pollution agents. Show the pullulating emissions of an MHD plant and a conventional steam plant. Thus an MHD plant offers great benefits in environment aspects of electric energy generation.
(7) It is possible to utilize MHD for peak power applications and emergency service (upto 100 hour per year). It has been estimate that MHD equipment for search duties is simpler, has the capability of operating in large unit sizes and the ability to make rapid start to full load.
What is MHD Power Generation ( Open cycle and working fluid)
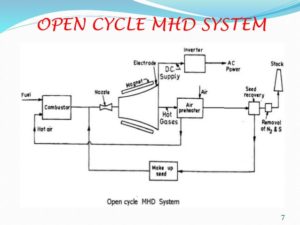
MHD system may be an open cycle system or a closed cycle system. In an open cycle system the working fluid is used on the once through basis. The working fluid after generating electrical energy is discharge to the atmosphere through a stack. In a closed cycle system the working fluid is recycled to the heat source and thus used again and again. The operation of MHD generators directly on combustion products is an open cycle system. The working fluid is air. In closed cycle system helium or argon is used as the working fluid. The use of a nuclear reactor using solid fuel element for providing the heat energy for an MHD process requires that the working fluid should have the following three properties (i) it should be capable of providing heat transfer under reactor operating condition (ii) it should not require excessive compressor work (iii) it should not be rendered active within the reactor. Helium, most nearly, fulfill all these requirements.
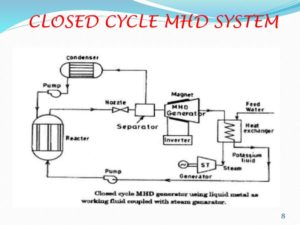
MHD Power Generation Closed cycle
For efficient practical realization an MHD system must have following features:
MHD power generation feature are these…
(1) Air superheating arrangement to heat the gas to around 2500 C so that the electrical conductivity of the gas is increased.
(2) The combustion chamber must have low heat losses.
(3) Arrangement to add a low ionization potential seed material t other gas to increase its conductivity.
(4) Water cooled but electrically insulating expanding duct with long life electrodes.
(5) A magnet capable of producing high magnetic flux density (5to 7 teslas).
(6) Seed recovery apparatus-necessary for both environment and economic reasons
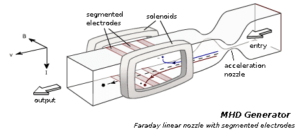
MHD Power Generation Open loop Cycle system
The closed cycle inert gas MHD system was conceived around 1965. Ti was thought that in this in this method all the advantage of the open cycle system would be retained and the main disadvantages of the open cycle system (viz. very high temperature requirements and a very chemically active flow) could be removed. As the name suggest, the working fluid, in a closed cycle, is circulated in a closed loop. The working fluid is helium or argon with cesium seeding.
The working fluid is a mixture of atomic gases, without rotational and vibration modes. That interacts readily with thermal electrons. Therefore it is possible in closed cycle system to maintain the conduction electron in the flow at a higher temperature than the bulk gas. Since electron density tent to be governed temperature rather than gas temperature we can get substantially higher electron density and electrical conductivity than would exist at the same temperature in combustion gas flow.
The possibility of using a nuclear heat source with a closed cycle MHD system has also been investigated. However its feasibility has yet not been established.
Hence these are MHD power generation and their open cycle and closed loop cycle system . if you find any incorrect in above article you must comment below in comment box.
If you want to know more about the What is MHD power generation you must watch this video.